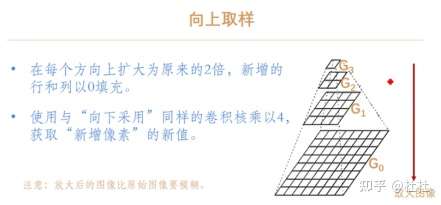
30.图像金字塔

同一图像的不同分辨率的子图集合。PS：向上采样与向下采样不是互逆操作(经过两种操作无法恢复原有图像)。

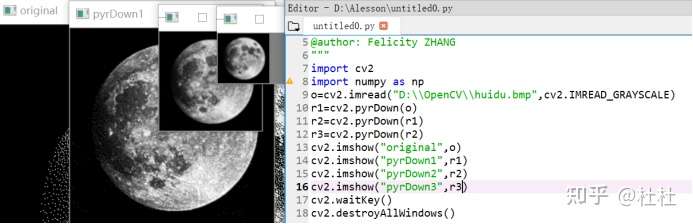
31.向下取样函数及使用

dst=cv2.pyrDown(scr)

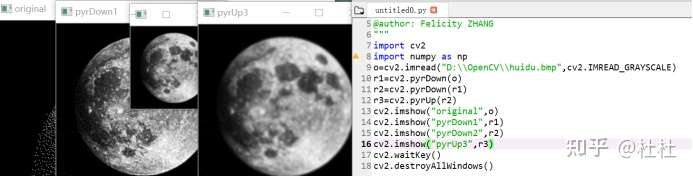
32.向上取样函数及使用

dst=cv2.pyrUp(scr):清晰度降低

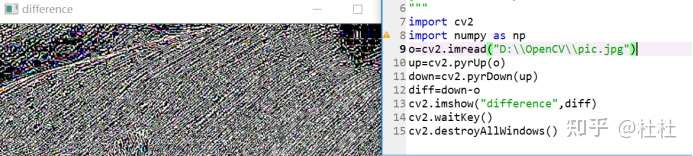
不可逆说明：两幅图的差异显示

33.拉普拉斯金字塔

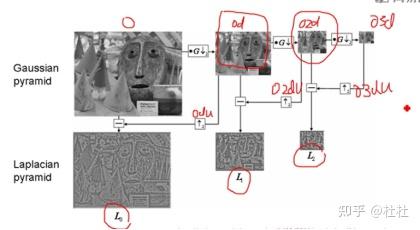
34.图像轮廓

边缘是不连续的，将边缘连接成整体即为轮廓；

Opencv里背景颜色为黑色前景颜色为白色；

cv2.findContours();%查找图像轮廓函数

image:修改后的原始图像

contours:轮廓

hierarchy:图像拓扑信息(轮廓层次)

括号内：

image:原始图像

mode:轮廓检索模式

method:轮廓的近似方式

cv2.drawContores();%将查找到的轮廓绘制到图像上

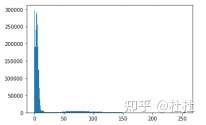
35.直方图

横坐标：图像中各个像素点的灰度级；纵坐标：具有该灰度级的像素个数

归一化直方图----纵坐标：出现该灰度级的概率

DIMS:使用参数的数量(一般等于1)；BINS：参数子集的数目；RANFE：统计灰度值的范围，一般为[0,255]

36.使用OpenCV统计直方图

channels:输入图像时灰度图时值为0，彩色图像可以是[0],[1],[2]分别对应BGR

mask:统计整幅图像直方图设为None,统计图像某一部分直方图时需要掩码图像

accumulate:默认值为false如果被设置成true则直方图在开始分配时不会被清零，多个直方图累积结果用于对一组图像计算直方图

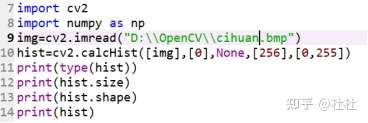
数组类型，得到256行1列的数据；

37.绘制OpenCV统计直方图

绘制普通函数图像

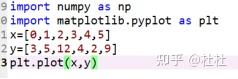
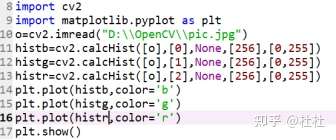
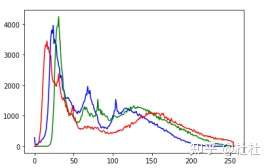
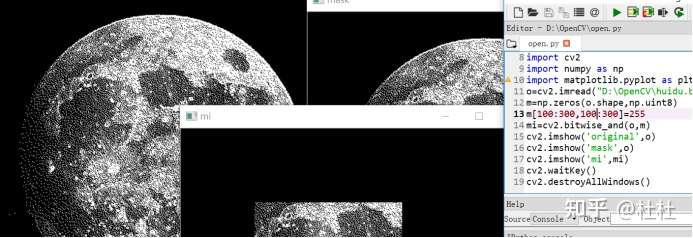
38.使用掩膜的直方图

mask=np.zeros(image.shape,np.uint8)

mask[200:400,200:400]=255

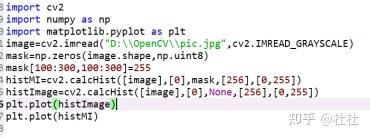
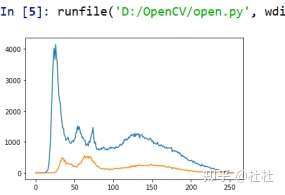
39.掩膜原理及演示

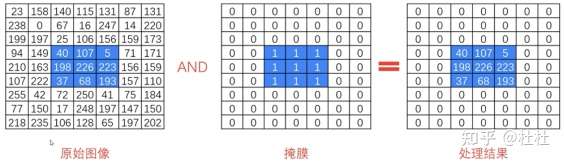
生成掩膜图像：maked_img=cv2.bitwise_and(imag,mask)

40.直方图均衡化原理

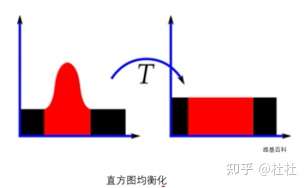
算法：

（1）计算累计直方图

（2）将累计直方图进行区间转换

（3）在累计直方图中，概率相近的原始值会被处理为相同值

3位位图：000~111(共7个)

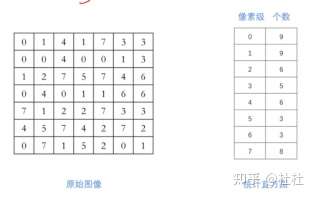
个数除以7*7得到百分比

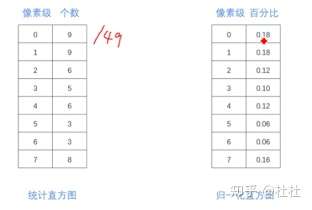
百分比累计得到累积直方图

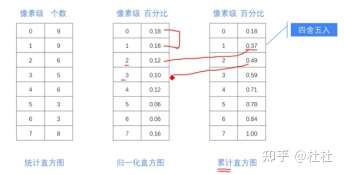
乘以7(0-7最大值为7)得到新的结果

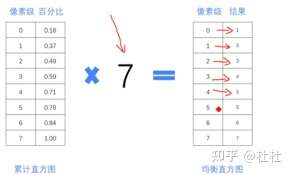
将灰度级变到256，乘以255(0-255最大)得到新结果

41.直方图均衡化函数：equalizeHist

dst=cv2.equalizeHist(scr)

42.subplot函数的使用

subplot(2,3,4)当每一个参数都小于10，可以直接书写3个数字subplot(234)

43.matplotlib.pyplot.imshow函数的使用

44.直方图均衡化对比

45.傅里叶变换的理论基础

任何连续的周期信号可以由一组正弦曲线组合而成(所有周期信号都可以表示成频域)

相位：不是同时开始的一组余弦函数，在叠加时要体现开始时间

46.numpy实现傅里叶变换

numpy.fft.fft2---实现傅里叶变换，返回一个复数数组；

numpy.fft.fftshift—将零频率分量移到频谱中心：

20*np.log(np.abs(fshift))—设置频谱的范围，将复数数据映射到[0,255]

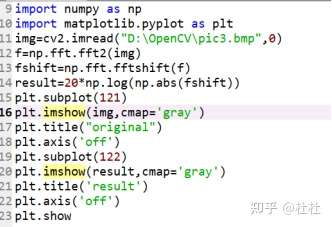
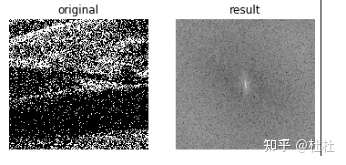
傅里叶得到低频高频信息(左上角为低频信息通过fftshift将低频移到中心)，针对低频，高频处理能够实现不同目的。傅里叶过程可逆，图像经过傅里叶变换，逆傅里叶变换能够恢复到原始图像(但图像可能会失真)。在频域对图像进行处理，在频域的处理会反映在逆变换图像上。

47.numpy实现逆傅里叶变换—从频谱得到图像

逆操作的原因：为了在频域对图像进行处理实现特定目的然后反映到原始图像(只保留低频-低通滤波(只保留细节)，只保留高频-高通滤波(细节被处理到)

numpy.fft.ifft2----ifft2为ifft逆函数

numpy.fft.ifftshift—ifftshift为fftshift逆函数，将频率从中心移到左上角

iimg=np.abs(逆傅里叶变换结果)—逆傅里叶变换的结果也是复数形式，将其映射到[0,255]

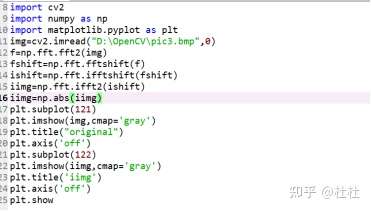
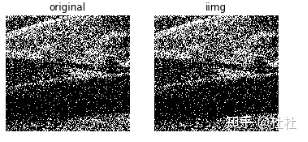
48.在频域进行高通滤波

低频对应图像内变换缓慢的灰度分量-草原上颜色趋于一致的草原；

高频对应图像内变化越来越快的灰度分量-草原上狮子边缘信息；

滤波：接受(通过)或者拒绝一定频率的分量；

通过低频的滤波器称为低通滤波器：将模糊一副图像；

通过高频的滤波器称为高通滤波器：将增强尖锐的细节，会导致对比度降低；

频域滤波：修改傅里叶变换以达到特殊目的(图像增强，压缩，去噪…)然后计算逆傅里叶变换返回图像域；

将中心低频信息进行覆盖：

49.OpenCV实现傅里叶变换

傅里叶变换：返回结果=cv2.dft(原始图像，转换标识)

频谱转换：numpy.fft.fftshift：将零频率转换到中心；

显示：返回值=cv2.magnitude(参数1.参数2)；

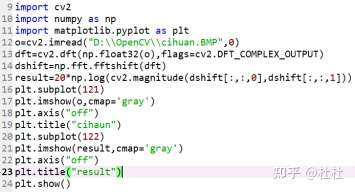
50.Opencv实现逆傅里叶变换

返回结果=cv2.idft(原始数据)

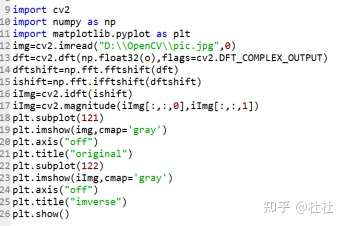
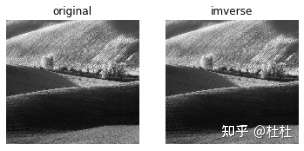
51.低频滤波演示

低频：细节，高频：边缘